| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- HTML
- 영국석사
- matplotlib
- 코딩공부
- for반복문
- 결정트리
- 파이썬
- 코드잇
- 코딩
- CSS
- 윈도우함수
- 유학생
- 로지스틱회귀
- 다항회귀
- 코드잇TIL
- Seaborn
- 선형회귀
- 나혼자코딩
- 런던
- sql연습문제
- SQL
- 코드잇 TIL
- numpy
- 데이터분석
- 판다스
- 오늘도코드잇
- 행렬
- 경사하강법
- 머신러닝
- 코딩독학
- Today
- Total
영국 척척석사 유학생 일기장👩🏻🎓
(데이터분석) Q1, Q3, 이상값 본문

1) Q1, Q3 구하기
데이터의 50% 지점을 의미하는 것이 중간값입니다. 이를 이용하면 Q1(데이터의 25%지점), Q3(데이터의 75%지점) 을 구할 수 있습니다. 예를 들어, 아래의 데이터에서 중간값은 86 입니다.
32, 48, 56, 78, 86, 96, 100, 120, 156
이 데이터를 중간값을 기준으로 둘로 나누었을 때, 첫번째 값부터 중간 값까지, 중간 값부터 마지막 값까지 둘로 나누었을 때, 왼쪽 묶음에서 의 중간값인 56이 25%에 해당하는 Q1값이라고 볼 수 있습니다. 반대로 오른쪽 묶음에 있는 중간값 100은 75% 지점, 즉 Q3이 됩니다.
하지만, 아래와 같이 Q1, Q2, Q3의 위치를 딱 정할 수 없는 경우도 있습니다. 데이터의 개수가 짝수일 때 중간값(Q2)를 구하려면 가운데에 있는 두 값의 합을 2로 나눠주면 됩니다. 즉, (24+35)/2 = 29.5 가 됩니다.
7, 15, 20, 24, 35, 57, 63, 125
먼저, Q1이 몇 번 인덱스에 있는 값인지 구합니다. 데이터에서 특정 퍼센트 지점의 인덱스를 구하기 위해서는 데이터의 개수에서 1을 뺀 뒤, 여기에 원하는 숫자를 곱해주면 됩니다. 위에서 데이터의 개수가 총 8개니까, (8-1)*0.25 = 1.75 라는 결과물을 얻을 수 있습니다. (데이터 개수에서 1을 빼는 건 파이썬에서 인덱스가 0부터 시작하니까 이를 보정해주기 위한 것입니다.)
그러면, 정수가 아닌 1.75번 인덱스에 있는 숫자는 어떻게 구해야 할까요? 일단, 1.75번 인덱스는 1번 인덱스에 있는 15와 2번 인덱스에 있는 20사이에 있다고 볼 수 있습니다. 즉, 1.75에서 정수부분인 1이 의미하는 것입니다. 그러면, 나머지 소수부분인 0.75의 의미는 무엇일까요? 소수 부분은 두 값 사이에서 정확히 어느 정도 위치에 있는지를 의미한다고 볼 수 있습니다. 0.75를 분수로 표현하면 4분의 3인데 즉, Q1은 15와 20 사이에서 4분의 3 지점에 위치하고 있습니다. 즉, 15+(20-15)*0.75 = 18.75가 됩니다.
Q3를 계산해 보겠습니다. Q3의 인덱스는 (8-1)*0.75 = 5.25입니다. 즉, 57(5번 인덱스)과 63(6번 인덱스) 사이에서 4분의 1지점에 위치한 값입니다. 즉, 57+(63-57)*0.25 = 58.5가 됩니다.
2) 이상값 구하기
박스 플롯에서 박스와 위스커 바깥에 있는 점들을 이상점(outlier)라고 합니다. 딱 봤을 때 다른 값들에 비해 유독 크거나 작은 값들을 이상점이라고 판단할 수도 있겠지만, 이게 이상점인지 아닌지 애매한 경우도 있습니다.
이상점을 구분하기 위한 기준들 중 가장 대표적인 것은 위에서 구한 Q1과 Q3 값을 활용하는 방법이 있습니다. 이 방식을 사용하면 먼저 Q3과 Q1 사이의 거리를 알아야 합니다. Q3에서 Q1을 빼주면 되고 이 값을 IQR(Interquartile Range)라고 합니다. 위의 데이터에서 Q3(58.5)에서 Q1(18.75)를 뺀 39.75가 됩니다.
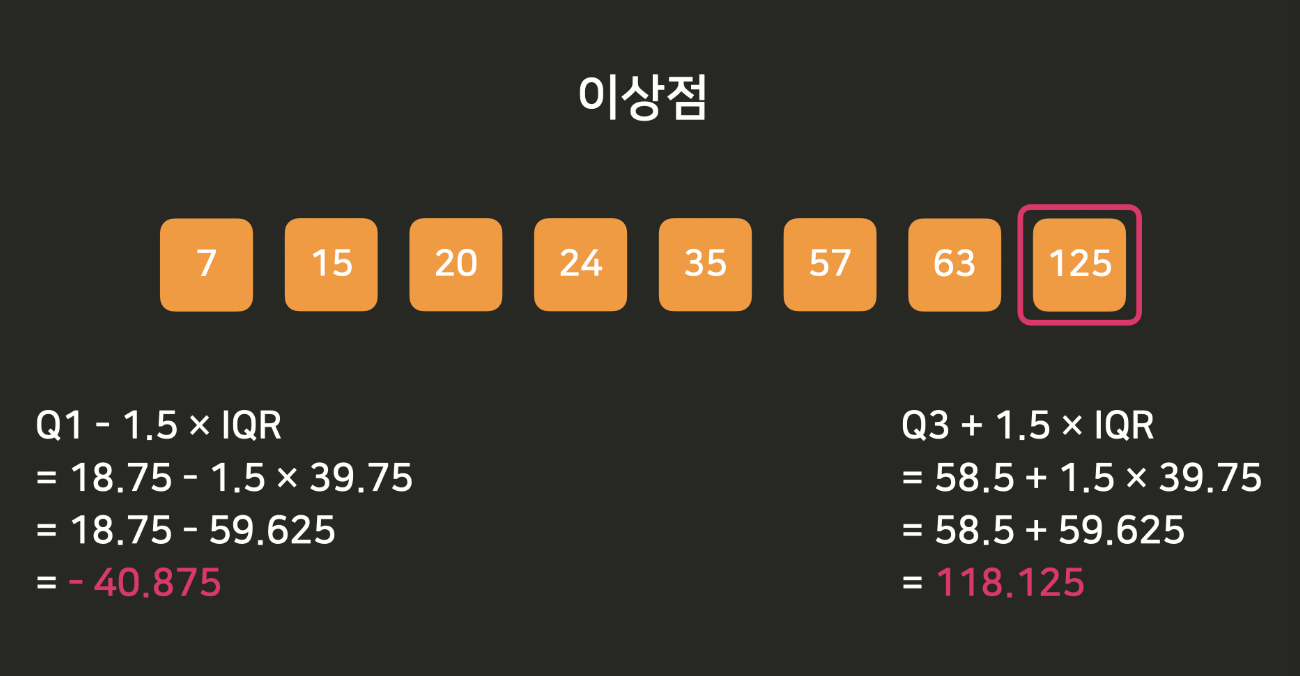
여기서 보통 Q1 지점에서 아래로 1.5*IQR 더 떨어져 있거나, Q3 지점에서 위로 1.5*IQR 떨어져 있는 값은 이상점이라고 판단합니다. 아까 Q1과 Q3을 구한 데이터를 예로 들면, 이상값이라고 판단하는 기준점은 -40.875와 118.125가 됩니다. 따라서 125가 이상점이라고 볼 수 있습니다.
'코딩공부 > Data analysis' 카테고리의 다른 글
| (데이터분석) 파이썬의 requests 라이브러리 이용하여 파일 다운로드하기 (0) | 2024.05.10 |
|---|---|
| (데이터분석) 파이썬의 zipfile 이용하여 플랫파일 압축 해제하고 읽기 (0) | 2024.05.09 |
| (데이터분석) pandas DataFrame 인덱싱 문법 정리 (0) | 2023.06.06 |
| (데이터분석) pandas의 데이터 타입 (0) | 2023.06.01 |
| (데이터분석) numpy 기본 통계 (0) | 2023.06.01 |




