| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 경사하강법
- 로지스틱회귀
- numpy
- 코딩
- 런던
- 데이터분석
- HTML
- 파이썬
- 판다스
- 윈도우함수
- 코드잇TIL
- 나혼자코딩
- 유학생
- 선형회귀
- 코드잇 TIL
- sql연습문제
- 영국석사
- 행렬
- 결정트리
- 코딩공부
- 다항회귀
- matplotlib
- 코딩독학
- 머신러닝
- for반복문
- 오늘도코드잇
- Seaborn
- SQL
- CSS
- 코드잇
- Today
- Total
영국 척척석사 유학생 일기장👩🏻🎓
(Machine Learning) 로지스틱 회귀 본문

선형 회귀를 이용해서 분류를 할 수 있긴 하지만, 선형 회귀는 예외적인 데이터에 너무 민감하게 반응한다는 단점이 있습니다. 그래서 분류를 할 때는 보통 선형 회귀 대신 '로지스틱 회귀(logistic regression)'을 사용합니다.
1. 로지스틱 회귀
로지스틱 회귀와 선형 회귀의 차이점을 알아봅시다. 데이터가 있으면 선형 회귀는 여기에 가장 잘 맞는 직선을 찾는 것입니다. 즉 일차함수를 찾는 것입니다. 로지스틱 회귀는 데이터에 가장 잘 맞는 일차함수가 아니라 데이터에 가장 잘 맞는 시그모이드 함수를 찾는 것입니다.
2. 시그모이드 함수
시그모이드 함수 식은 아래와 같습니다.
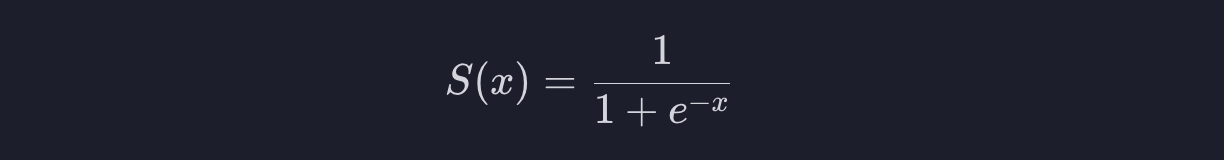
그래프로 그리면 아래와 같이 생겼습니다.

시그모이드 함수의 가장 중요한 특징은, 무조건 0과 1사이의 결과를 낸다는 것입니다.
x가 엄청 커서 무한대로 간다고 합시다. 시그모이드 식에서 x에 무한대를 대입하면 1로 수렴하게 됩니다.
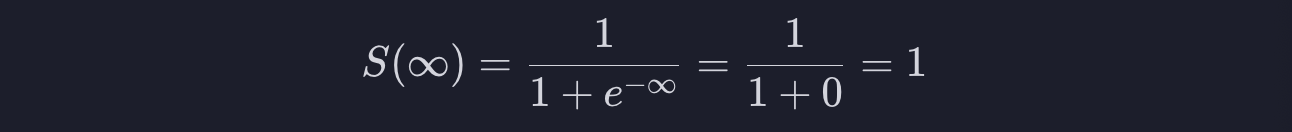
반대로 x가 마이너스 무한대로 간다고 합시다. x에 마이너스 무한대를 대입하면 0으로 수렴하게 됩니다.
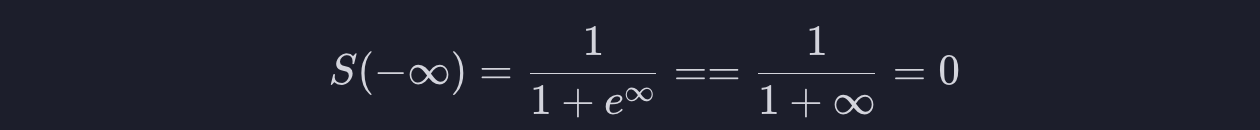
결과적으로 x가 엄청나게 작으면 0에 가까우지고, x가 엄청나게 크면 1에 가까워진다는 것입니다. 그래서 시그모이드 함수는 항상 0과 1사이의 결과를 내개 됩니다.
우리가 선형 회귀에서 쓰는 가설 함수는 일차함수 입니다. 일차 함수 같은 경우에는 결과가 얼마든지 작아질 수 있고 또 얼마든지 커질 수 있기 때문에 분류를 하기엔 부적합합니다. 반면 시그모이드 함수의 결과는 항상 0과 1사이에 떨어지기 때문에 분류를 할 때 더 유용하게 쓸 수 있습니다.
선형 회귀는 예외적인 데이터 하나에 가설 함수가 너무 민감하게 반응합니다. 그런데 시그모이드 함수는 그 문제를 해결해 줍니다. 시그모이드 함수는 아래와 같이 생겼기 때문에 많이 동떨어진 데이터 하나가 있어도 크게 영향을 받지 않는 것입니다.
3. 가설 함수
로지스틱 회귀를 하기 위해서는 로지스틱 회귀에서 사용할 가설 함수를 알아야 합니다.
일단 가설 함수란, 특정 데이터에 대해서 입력 변수를 받으면 목표 변수를 예측해 주는 함수입니다. 선형 회귀에서는 아래와 같이 생겼습니다.
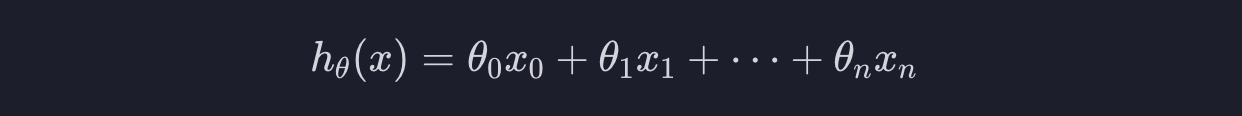
벡터를 사용하면
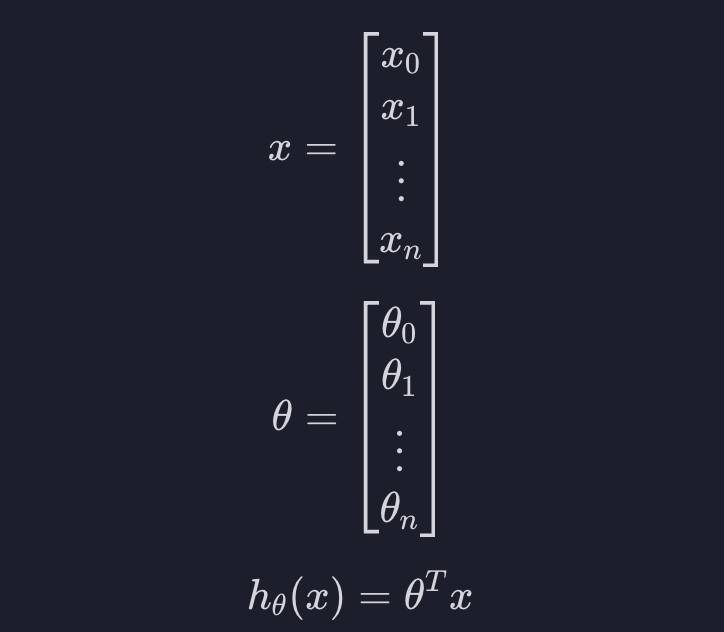
선형 회귀에서 썼던 이 가설 함수를 조금 발전시키면 로지스틱 회귀의 가설 함수가 나옵니다. 로지스틱 회귀의 가설 함수도 h라고 해야 하니까 이건 h말고 g라고 합시다.
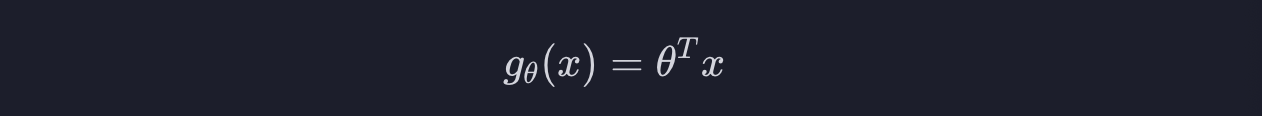
그러고 나면 로지스틱 회귀의 가설 함수는 이렇게 쓸 수 있습니다.
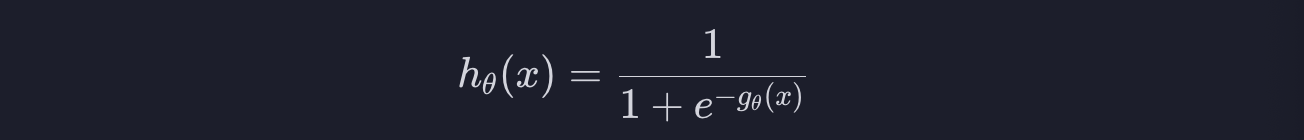
여기서 함수 g를 대입하면 아래와 같습니다.
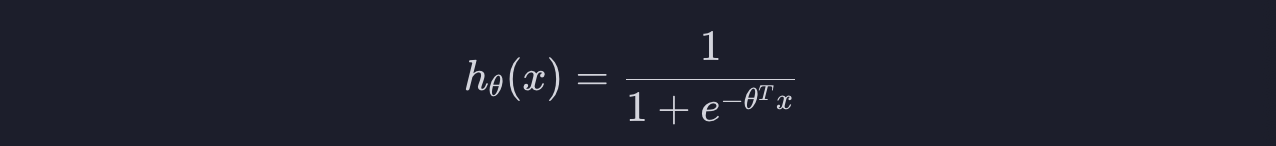
좀 더 해석해봅시다.
함수 g는 일차 함수 입니다. 일차 함수는 아웃풋이 엄청 클 수도 있고, 엄청 작을 수도 있습니다. 예를 들어서 일차 함수가 이런 직선이라면 인풋이 엄청 커지거나 엄청 작아지면 결국 아웃풋도 엄청 커지거나 엄청 작아질 수 있습니다.
그런데 로지스틱 회귀를 할 때 우리는 아웃풋이 항상 0과 1사이에 떨어지도록 하고 싶습니다. 그러기 위해서 시그모이드 함수를 쓰면 됩니다.

이 함수를 쓰면 어떤 인풋을 넣든 간에 아웃풋은 무조건 0과 1사이에 떨어집니다.
선형 회귀에서 썼던 가설 함수인 g의 아웃풋을 이 시그모이드 함수의 인풋으로 집어 넣으면 결국 0과 1 사이의 결과만 나옵니다.
4. 가설 함수의 아웃풋
그렇다면 0과 1 사이의 수로 무엇을 하는 것일까요?
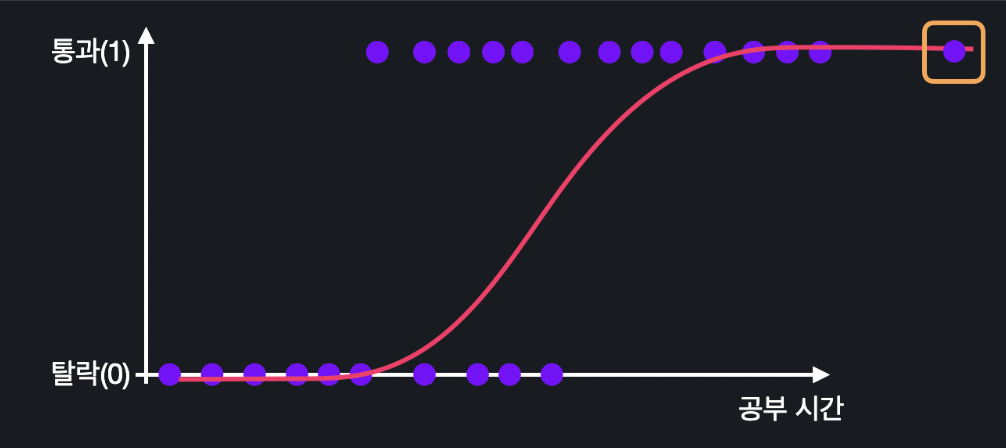
이 가설 함수가 하는 일이 공부한 시간을 바탕으로 시험을 통과할 지 예측하는 거라고 합시다. 0은 통과 못하는 걸 의미하고 1은 통과하는 걸 의미합니다.

여기서 x_0은 항상 1이니까 그냥 무시하면 되고 x_1이 50이라는 건 학생이 50시간 공부했다는 걸 의미합니다.
x를 가설 함수에 넣었더니 0.9가 나왔다는 의미는 목표 변수가 1일 확률이 0.9, 즉 90%라는 의미입니다. 그러니까 50시간을 공부한 학생이 시험을 통과했을 확률은 90%라는 거죠. 확률이 50%가 넘으니까, 분류를 하자면 이 학생은 통과한 학생으로 분류하면 되는 겁니다. 만약 아웃풋이 0.4라면 통과할 확률이 40%라는 거니까, 통과하지 못한 걸로 분류하면 되는 것입니다.
5. 로지스틱 회귀의 목적
단순하게 입력 변수가 하나라고 해봅시다. 우리가 하려는 건 주어진 데이터에 가장 잘 맞는 시그모이드 모양의 곡선을 찾아내는 것입니다.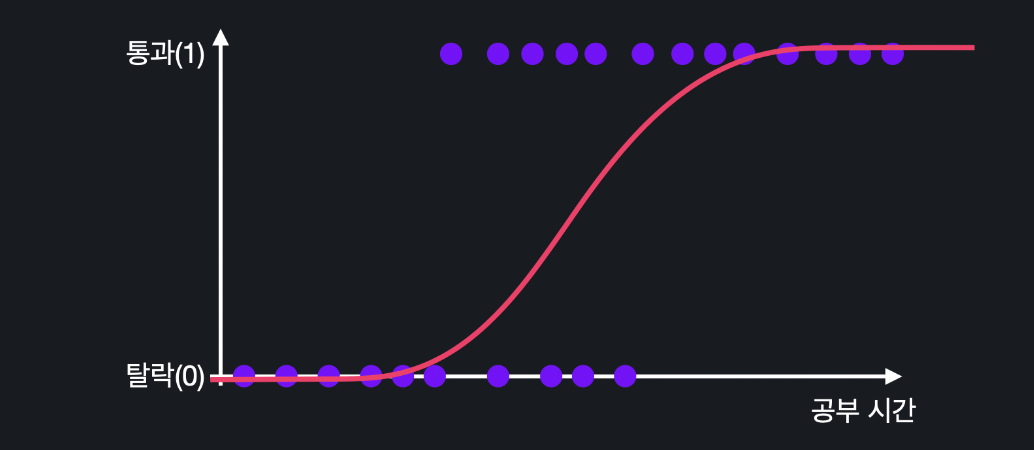
이 곡선을 어떻게 찾을 수 있을까요? theta 값들을 조절해서 찾는 것입니다. 변수가 하나라는 건 theta 값이 theta0, theta1 이렇게 두개가 있다는 것입니다. 이 때 가설 함수를 아래와 같이 표현할 수 있습니다.
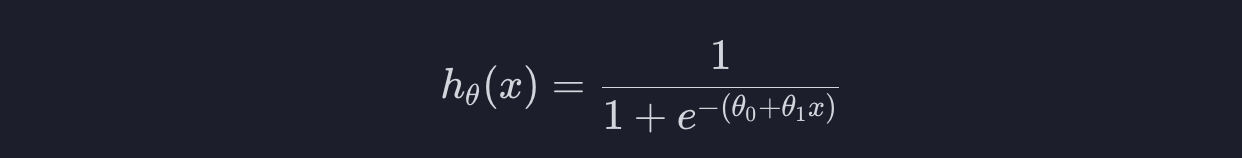
theta0의 값을 늘리면 곡선이 왼쪽으로 움직이고, 줄이면 오른쪽으로 움직이는 것입니다.
theta1의 값을 늘리면 S모양의 곡선이 조여지고, 줄이면 늘어지고 이렇게 됩니다.
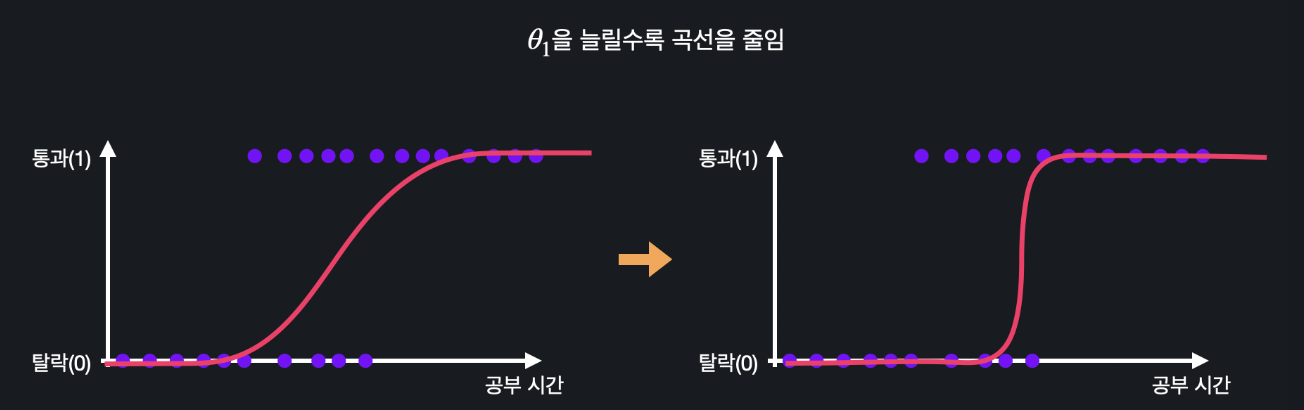
선형 회귀와 똑같이 이렇게 theta0과 theta1의 값들을 바꿔가면서 갖고 있는 학습 데이터에 가장 잘 맞는 시그모이드 모양의 곡선을 찾아내는 게 로지스틱 회귀의 목적인 것입니다.
선형 회귀와 마찬가지로 입려 변수가 여러 개면 시각화하기 힘들어집니다. 어떻게 하면 최적의 theta값들을 찾을 수 있는지, 다음 글에서 알아봅시다.
'코딩공부 > Machine Learning' 카테고리의 다른 글
| (Machine Learning) 로지스틱 회귀 로그 손실, 손실 함수 (0) | 2023.09.13 |
|---|---|
| (Machine Learning) 로지스틱 회귀 결정 경계 (0) | 2023.09.12 |
| (Machine Learning) 분류 (0) | 2023.09.12 |
| (Machine Learning) 다중 다항 회귀 (0) | 2023.09.08 |
| (Machine Learning) 단일 속성 다항 회귀 (0) | 2023.09.08 |




