| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 코딩공부
- 코드잇
- 로지스틱회귀
- 경사하강법
- 다항회귀
- 코드잇 TIL
- 윈도우함수
- 판다스
- sql연습문제
- 머신러닝
- SQL
- Seaborn
- 나혼자코딩
- 코드잇TIL
- 파이썬
- numpy
- CSS
- 런던
- 오늘도코드잇
- 행렬
- 유학생
- 결정트리
- for반복문
- matplotlib
- HTML
- 영국석사
- 코딩
- 코딩독학
- 선형회귀
- 데이터분석
- Today
- Total
영국 척척석사 유학생 일기장👩🏻🎓
(Machine Learning) L1, L2 정규화 (Regularization) 본문
(Machine Learning) L1, L2 정규화 (Regularization)
life-of-nomad 2023. 9. 20. 10:17
저번 글에서 설명하였듯이 복잡한 모델을 그대로 학습시키면 '과적합'이 됩니다. '정규화'라는 기법은 학습 과정에서 모델이 과적합되는 것을 예방해 줍니다.
1. 정규화
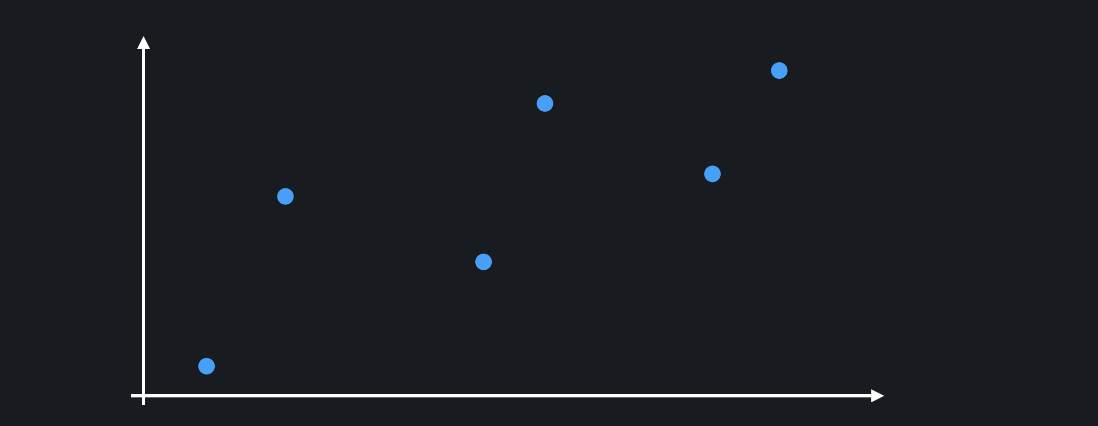
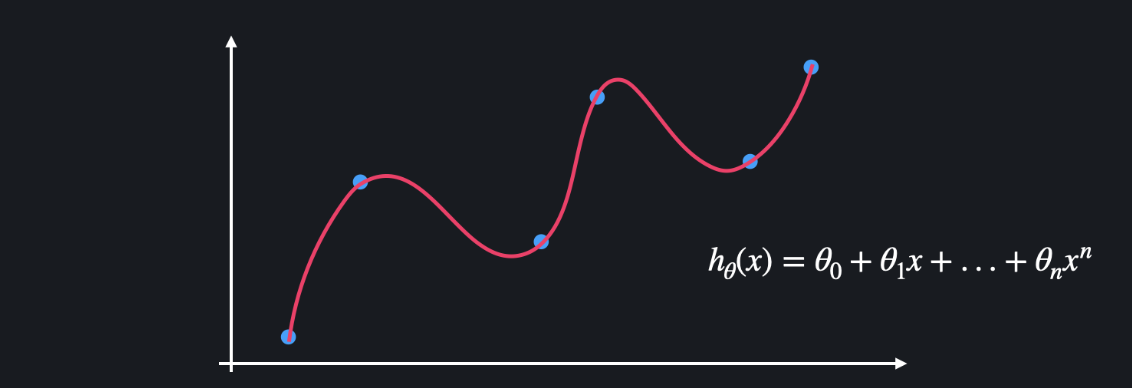
위와 같은 학습 데이터를 이용해서 다항 회귀를 하는 경우를 생각해봅시다. 모델이 과적합돼서 아래와 같은 복잡한 다항 함수가 나왔다고 해봅시다.
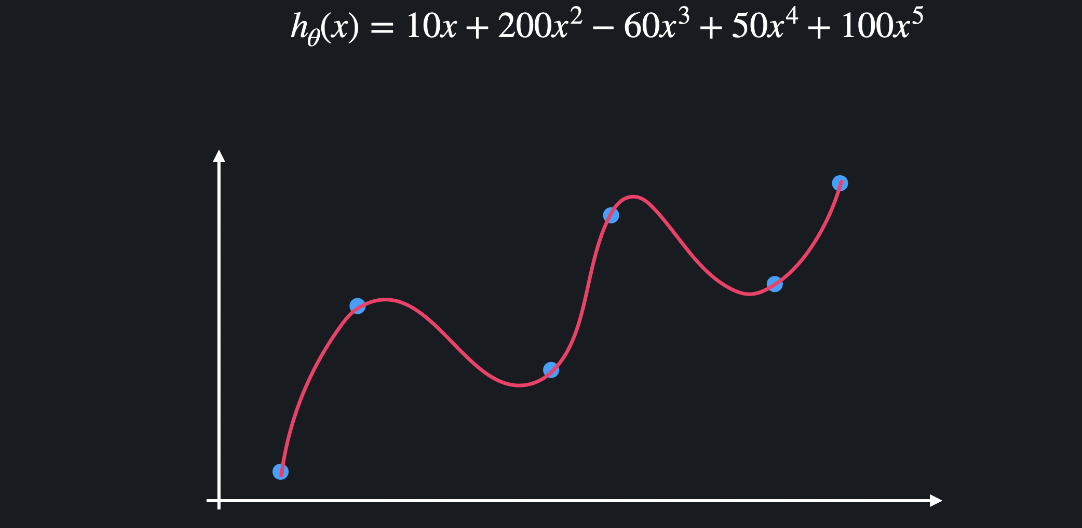
과적합된 함수는 보통 위아래로 엄청 왔다갔다 하는 특징이 있습니다. 많은 굴곡을 이용해서 함수가 training 데이터를 최대한 많이 통과하도록 하는 것입니다. 함수가 이렇게 급격하게 변화한다는 것은 함수의 계수, 즉 가설함수의 세타 값들이 굉장히 크다는 뜻입니다.
정규화는 모델을 학습시킬 때 세타 값들이 너무 커지는 것을 방지해 줍니다. 세타 값들이 너무 커지는 걸 방지하면 training 데이터에 대한 오차는 조금 커질 수 있어도, 위아래로 변동이 엄청 심하던 가설 함수를 좀 더 완만하게 만들 수 있습니다.
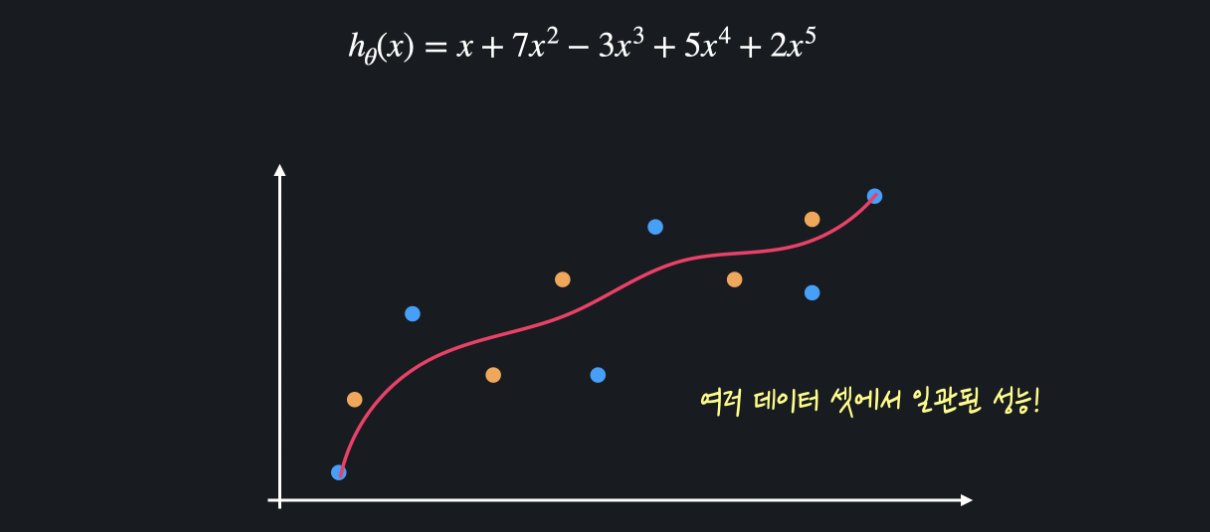
이런 함수는 여러 데이터 셋에 대해 더 일관된 성능을 보이기 때문에 과적합을 막을 수 있는 것입니다.
즉, 머신 러닝에서 정규화는 손실 함수에 '정규화 항' 이라는 것을 더해서 세타 값들이 커지는 것을 방지하는 기법입니다.
다항 회귀를 예시로 들어보겠습니다.

위 처럼 데이터에 가장 잘맞는 선 h를 찾는게 목표입니다. "데이터에 가장 잘 맞는다"라는 것은 데이터에 대한 평균 제곱 오차를 최소화한다는 뜻입니다. 평균 제곱 오차는 아래와 같이 계산합니다.
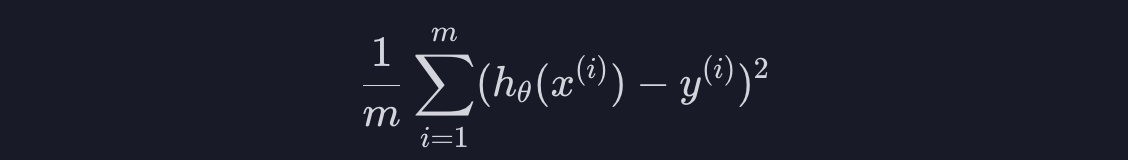
여기서 m은 데이터의 개수, h(x^(i))는 i번째 데이터의 (목표 변수의) 예측값, y^(i)는 i번째 데이터의 (목표 변수의) 실제 값을 나타냅니다.
그리고 계산의 편의를 위해 평균 제곱 오차를 2로 나눠주면 손실 함수 J가 나옵니다.
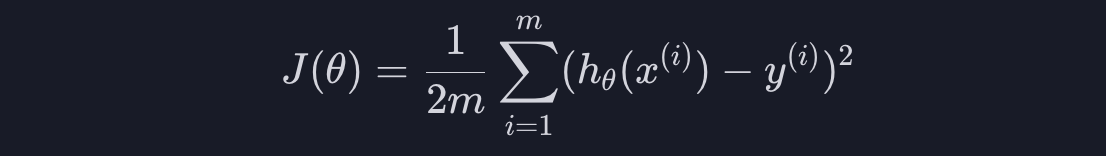
손실 함수는 일반적으로 '가설 함수를 평가하기 위한 함수'입니다. 손실 함수의 아웃풋이 작을수록 더 좋은 가설 함수고, 손실 하뭇의 아웃풋이 클수록 더 안좋은 가설 함수라고 할 수 있습니다. 위처럼 다항 회귀는 평균 제곱 오차를 손실 함수로 쓰니까 "training 데이터에 대한 평균 제곱 오차가 작을수록 좋은 가설 함수다" 라는 뜻입니다.
그런데 위 모델은 training 데이터에 대한 오차는 굉장히 작지만 test 데이터에 대한 오차는 굉장히 큽니다. 모델의 세타 값들이 너무 커서 training 데이터에 과적합이 된 것입니다. 이 문제를 해결하기 위해서는 좋은 가설 함수의 기준을 조금 바꿔주면 됩니다. "training 데이터에 대한 오차도 작고 세타값들도 작아야 좋은 가설 함수다" 이렇게 바꿔주면 됩니다.
이걸 수학적으로 표현해 봅시다. 손실 함수 J는 값이 클수록 가설 함수가 안좋다는 뜻이기 때문에 아래와 같이 손실 함수에 세타값들의 절댓값, 또는 크기를 더해 주면 됩니다.
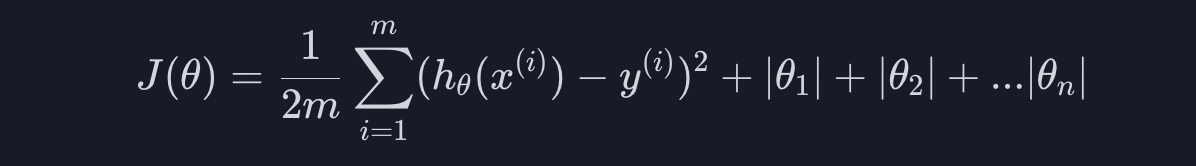
여기서 주의해야 할 점은 세타0은 과적합과 상관이 없기 때문에 세타0의 절댓값은 더해주지 않습니다.
위 식을 줄여서 쓰면 아래와 같습니다.

i가 1부터 n의 값을 가지면서 시그마 안에 있는 항을 더해줍니다. 이 뒤 부분을 정규화 항이라고 합니다.
손실 함수를 이렇게 정의하면 세타값들이 커질수록 손실 함수도 커지고, 세타값들이 작아질수록 손실 함수도 작아집니다. 세타값들이 클수록 안 좋은 가설 함수고 세타 값들이 작을수록 좋은 가설 함수라는 뜻입니다.
예를 들어 아래와 같은 5차항 함수 2개가 있다고 해봅시다.
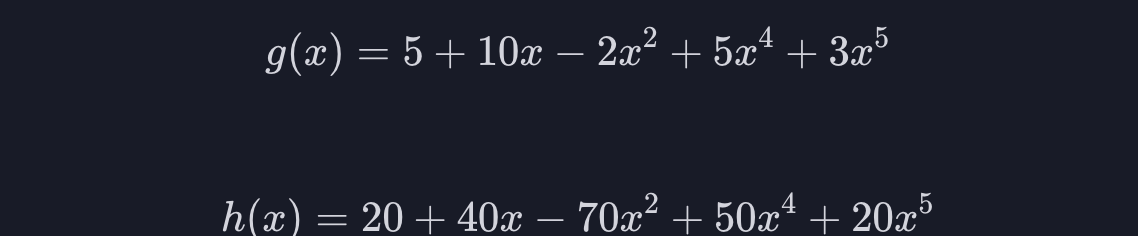
g의 정규화 항의 값은 10+2+5+2=20 이고, h의 정규화 항의 값은 40+70+50+20=180이 나옵니다. (상수항은 제외합니다.)
임의로 g의 평균 제곱 오차는 5, h의 평균 제곱 오차는 1이라고 하면 아래와 같은 손실 함수 표가 완성됩니다.
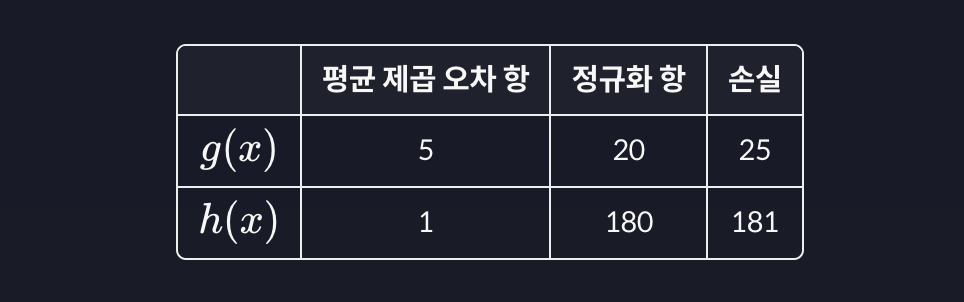
가설 함수 g는 데이터에 대한 평균 제곱 오차는 h보다 크지만 세타 값들이 훨씬 작기 때문에 더 좋은 가설 함수라고 평가하는 것입니다.
그런데 사실 정규화 항에는 아래와 같이 람다 라는 상수를 곱해줍니다.
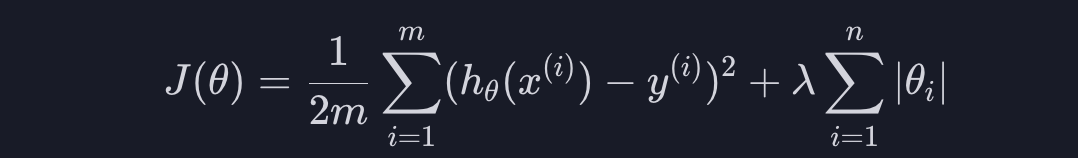
람다는 세타값들이 커지는 것에 대해서 얼마나 많은 패널티를 줄 건지를 정해주는겁니다. 예를 들어 람다가 100이면 세타 값들이 조금만 커져도 손실 함수가 굉장히 커지기 때문에 세타 값을 줄이는 게 중요하고, 람다가 0.01이면 세타값들이 커져도 손실 함수는 별로 안 커지기 때문에 평균 제곱 오차를 줄이는 게 중요한 것입니다.
위의 정규화 방식을 L1 정규화라고 합니다. 손실 함수에 정규화 항을 더해주는 것입니다.
그리고 L1 정규화를 사용하는 회귀 모델을 Lasso 모델이라고 합니다.
L2 정규화도 똑같은 개념인데 아래와 같은 정규화 항을 더해줍니다.
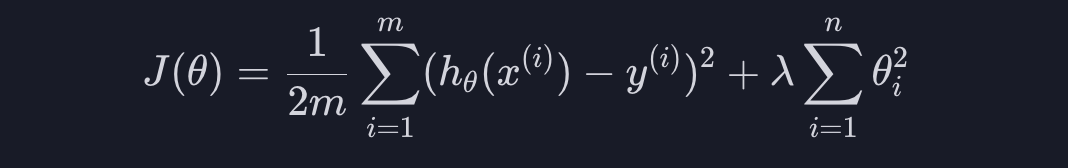
세타 값의 절댓값이 아닌 제곱 값을 더해주는 것입니다. L1 정규화와 마찬가지로 세타값들이 커지면 손실이 커지기 때문에 세타 값들이 커지는 것을 방지해 줍니다. L2 정규화를 사용하는 회귀 모델은 Ridge 모델이라고 합니다.
정리하자면, 손실 함수를 최소화시키려면 두 항을 모두 줄여야 하기 때문에 데이터에 대한 오차도 작고 세타값들도 작은 가설 함수를 찾을 수 있습니다.
데이터에 대한 오차와 세타 값 중 어떤 것을 줄이는 게 더 중요한지는 상수 람다에 따라 결정됩니다. 람다가 클수록 세타값을 줄이는 게 중요하고, 람다 값이 작을수록 데이터에 대한 오차를 줄이는게 중요한 것입니다.
2. L1, L2 정규화 차이점
- L1 정규화는 여러 세타값들을 0으로 만들어 줍니다. 모델에 중요하지 않다고 생각되는 속성들을 아예 없애줍니다.
- L2 정규화는 세타값들을 0으로 만들기 보다는 조금씩 줄여줍니다. 모델에 사용되는 속성들을 L1처럼 없애지는 않습니다.

위의 그림에서 각 막대는 어떤 모델의 세타값을 나타냅니다. 가장 위 그래프는 정규화를 사용하지 않고 찾은 세타값들, 중간 그래프는 L1 정규화를 사용해서 찾은 세타값들, 마지막 그래프는 L2 정규화를 사용해서 찾은 세타값들입니다.
L1 정규화는 여러 세타값들을 아예 0으로 만들어 버리고, L2 정규화는 전체저긍로 세타값들을 조금씩 줄여줍니다.
따라서 L1 정규화는 어떤 모델에 쓰이는 속성 또는 변수의 개수를 줄이고 싶을 때 사용됩니다. 예를 들어 속성 20개를 사용해서 2차 다중 다항 회귀 모델을 만든다면 속성은 총 230개가 됩니다.
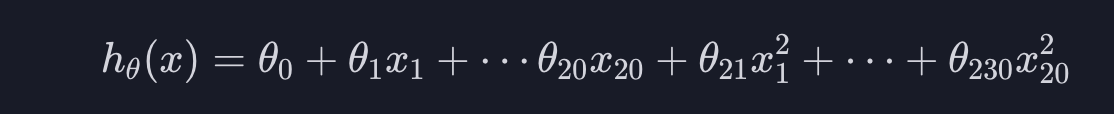
속성이 많으면 과적합뿐만이 아니라 모델을 학습시킬 때 많은 자원(RAM, 시간)을 소모할 수 있습니다. 이럴 때 L1 정규화를 사용하면 많은 세타값들을 0으로 만들어 주기 때문에 사용되는 속성의 개수를 많이 줄일 수 있습니다.
반대로 딱히 속성의 개수를 줄일 필요가 없다고 생각되면 L2 정규화를 사용하면 되는 것입니다.
'코딩공부 > Machine Learning' 카테고리의 다른 글
| (Machine Learning) 하이퍼 파라미터(Hyperparameter) 그리드 서치 (0) | 2023.09.22 |
|---|---|
| (Machine Learning) k-겹 교차 검증 (0) | 2023.09.21 |
| (Machine Learning) 편향(Bias)과 분산(Variance) 트레이드 오프(Tradeoff) (0) | 2023.09.18 |
| (Machine Learning) one-hot encoding (0) | 2023.09.18 |
| (Machine Learning) Feature Scaling 과 경사하강법 (0) | 2023.09.15 |




