| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 파이썬
- 코딩
- 로지스틱회귀
- sql연습문제
- 코딩공부
- 영국석사
- 데이터분석
- 윈도우함수
- HTML
- numpy
- 행렬
- SQL
- 결정트리
- 코드잇
- 코드잇TIL
- 판다스
- 머신러닝
- 오늘도코드잇
- 나혼자코딩
- 경사하강법
- Seaborn
- CSS
- matplotlib
- 다항회귀
- 코딩독학
- for반복문
- 유학생
- 선형회귀
- 코드잇 TIL
- 런던
- Today
- Total
영국 척척석사 유학생 일기장👩🏻🎓
(Machine Learning) Convex 함수 본문

1. convex 함수
경사 하강법, 정규 방정식을 이용하여 선형, 다중 회귀 손실 함수를 최소화시킬 수 있었습니다. 손실함수 J(theta)의 경사를 구한 뒤에 이걸 이용해서 최솟값을 갖는 theta를 찾았습니다. 그런데 단순히 경사 하강법과 정규 방정식만 이용하면 항상 손실 함수의 최소 지점을 찾을 수 있을까요? 예를 들어 봅시다.
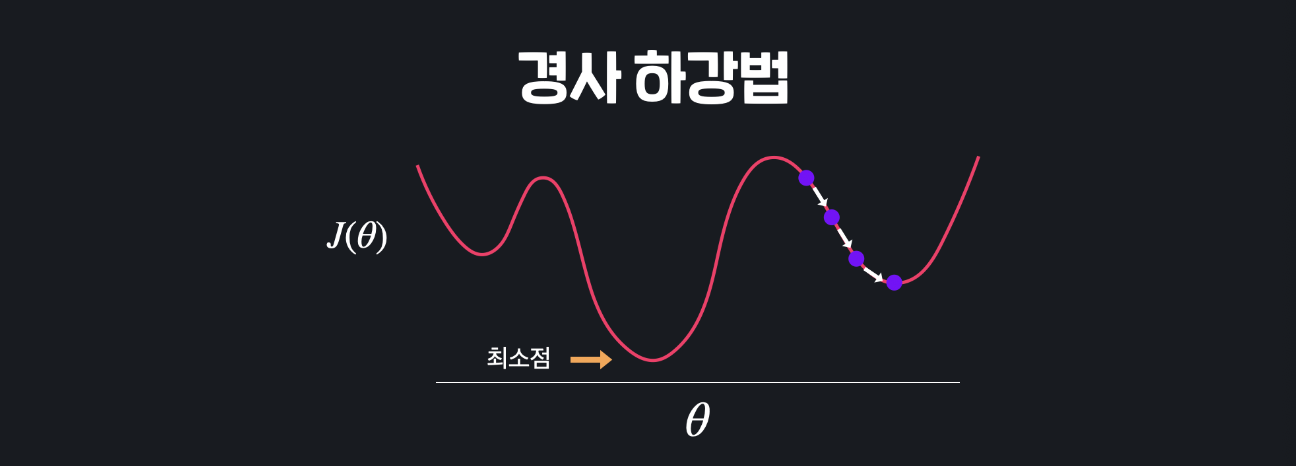
이 지점에서 시작을 해서 경사를 따라 쭉 내려갑니다. 내려가다 보면 어느 순간 여러 극소값 중 하나에 오겠죠? 그럼 여기서는 경사가 0이어서 경사 하강이 종료가 됩니다. 그럼 손실 함수의 최저점을 찾아갈 수가 없습니다.
정규 방정식도 마찬가지입니다.
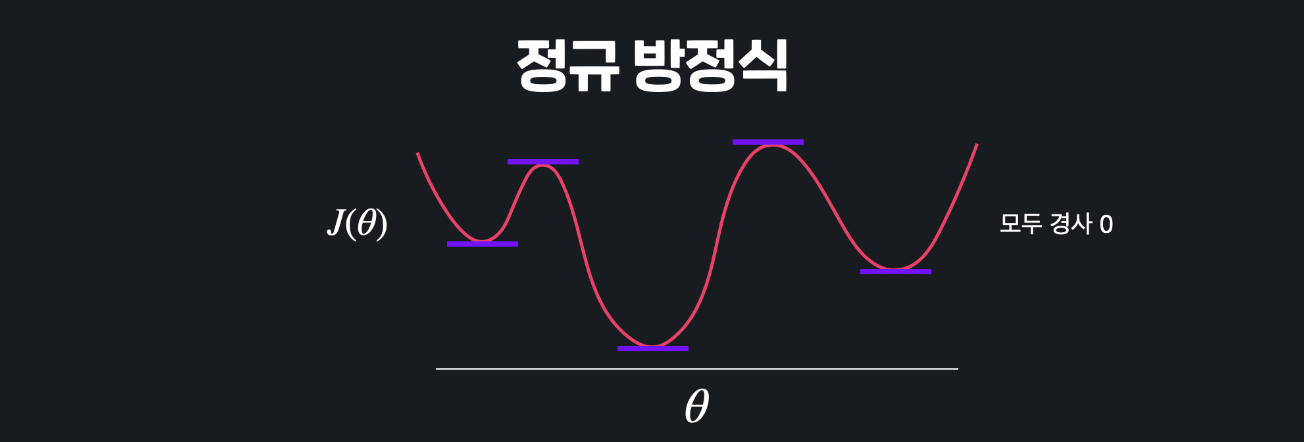
이렇게 수많은 극소값들과 극대값들이 있으면 아무리 방정식을 해결해도 구한 수많은 지점 중에서 어떤 지점이 최소점인지 알 수 없습니다. 이 모든 지점들이 경사가 0이니까요. 그러니까 함수가 이런 식으로 생긴 경우에는 경사 하강법과 정규 방정식을 통해서 구한 극소 지점이 손실 함수 전체에서 최소 지점이라고 확실하게 얘기할 수 없습니다.
반대로 아래와 같은 경우를 봅시다.
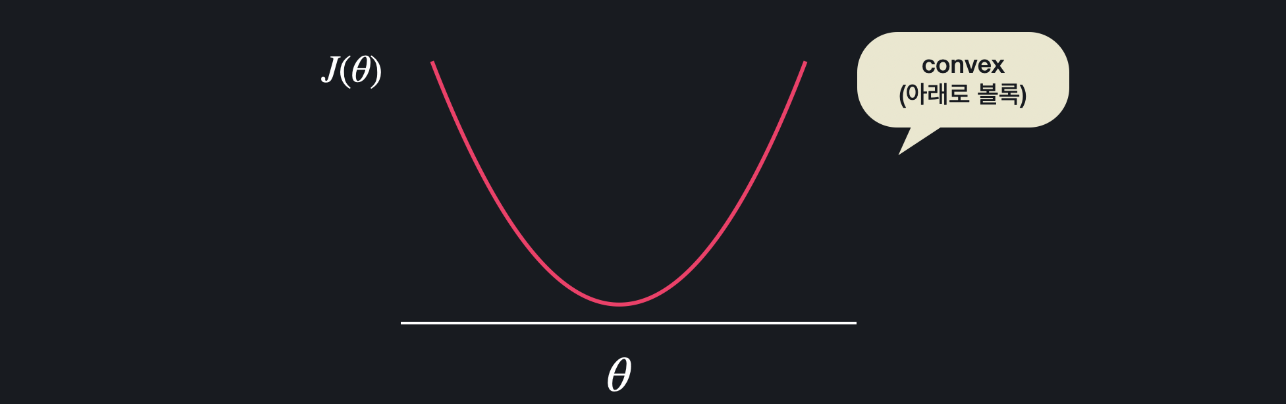
이 함수는 어떤 지점에서 경사 하강을 시작해도 항상 손실 함수의 최소 지점을 찾을 수 있고, 정규 방정식을 이용해서 최소점을 구할 수 있습니다. 이런 함수를 convex함수 (아래로 볼록한 함수)라고 합니다.
convex 함수에서는 항상 경사 하강법이나 정규 방정식을 이용해서 최소점을 구할 수 있는 반면, non-convex함수에서는 구한 극소점이 최소점이라고 확신할 수 없습니다.
2. 선형 회귀의 평균 제곱 오차
선형 회귀에서는 가정 함수의 예측값들과 실제 목표 변수들의 평균 제곱 오차(MSE)를 손실 함수로 사용했었습니다. 다행히 선형 회귀 손실 함수로 사용하는 MSE는 항상 convex함수입니다. 그러니까 선형 회귀를 할 때는 경사 하강법을 하거나 정규 방정식을 하거나 항상 최적의 theta 값들을 구할 수 있는 것입니다.
'코딩공부 > Machine Learning' 카테고리의 다른 글
| (Machine Learning) 단일 속성 다항 회귀 (0) | 2023.09.08 |
|---|---|
| (Machine Learning) 다항 회귀 (0) | 2023.09.07 |
| (Machine Learning) 경사 하강법 vs 정규 방정식 (0) | 2023.08.29 |
| (Machine Learning) 다중 선형 회귀 구현하기 (0) | 2023.08.22 |
| (Machine Learning) 다중 선형 회귀 경사 하강법 (0) | 2023.08.22 |




